About two months ago I had the opportunity to work with a class of struggling 8th graders in a support class. I chose to do the ticket option lesson with them and wanted to share my experiences and some student work samples. From my previous experiences working with these students, I knew they struggled mathematically but were somewhat willing to persevere if they were interested in the context. The teacher also informed me that they had already covered unit rates in her class this year (though I know it was also covered in 6th and 7th grade as well).
I began by passing out the Problem Solving Framework (which I am continuously refining) and the ticket booth picture. I explained how I took the picture below when I went to a carnival and wasn’t sure which tickets I should buy.
I then asked students the first three challenges at the same time (at this point I was still asking students the questions rather than having students come up with their own questions):
- Which ticket option is the best deal?
- Which ticket option is the worst deal?
- Which ticket options are the same deal?
This is where I encountered my first unexpected challenge. Students didn’t understand what “best” meant in this context. I assumed that everyone thought “best” meant the lowest cost per ticket. However to these students “best” meant “most tickets” and many students immediately wrote down that $50 for 120 tickets was the “best” deal without doing any additional work. I asked them why and they said that it was the deal that would give them the most tickets.
I decided to play dumb and present two ideas of “best” I was trying to figure out. Was 120 tickets for $50 the “best” deal because I got the most tickets or was 1 ticket for $.50 the “best” deal because I spent the least amount of money. A conversation ensued with students eventually concluding that both the quantity of tickets and the cost of the tickets mattered. They did not talk about combining them together in terms of a rate at this point.
I next asked them to fill out their Problem Solving Framework and explain “What problem are you trying to figure out?” Many students still stated that they wanted to know which deal would give them the most tickets. We did a think-pair-share to discuss what everyone had written. Eventually we discussed (again) what “best” meant. I will admit that I wasn’t loving that we had spent almost 15 minutes on just what the question was asking. The positive side was that I was able to bring this issue to light. This was something that was hindering their critical thinking and it could have sabotaged the lesson for some students if it wasn’t addressed.
From there I asked them to describe “What do you already know from the problem?” and “What do you need to know to solve the problem?” For the information that they already know, most students either rewrote the ticket price chart or stated that they knew the ticket prices. However, when I asked students to tell me about the information they need to know, they said:
- How many tickets will we use?
- How long will we be staying there?
- How many people are we going with?
- How many tickets do the rides cost?
Questions like these are actually quite common with real-world problem-based lessons. Clearly students were having trouble abstracting the context to simply explore the price per ticket. In real life we would be unlikely to use 120 tickets so we would not even consider that as an option. They had trouble letting go of this reality. I didn’t want to tell them that these questions were irrelevant so instead I told them that we will be staying there all day, that rides cost many tickets, and that we came with bunch of people. I made it clear to them that no matter how many tickets we buy, we will use them. We just want to find the “best” deal. It is worth wondering whether students would be able to get past this if this was a constructed response question on a CCSS assessment? Would they answer, “I don’t know until I know how long we will be staying at the carnival.”
With that completed, I set them free to try out the problem. Unfortunately students were still unsure of how to proceed. They could not come up with any strategy to analyze the data and struggled for about ten minutes. Most did not realize that they could buy the same ticket option repeatedly (for example, 2 sets of 25 tickets for $10 is better than 1 set of 50 tickets for $25). I was trying my best to, as Dan Meyer says, “be less helpful.” Clearly I could just tell them all to divide the price by the number of tickets to get the unit rate. If I did that it might even appear like they understood what to do . However it is also a great way to sweep their misunderstandings under the rug and not address them.
I decided to have a discussion about what would happen if you bought one ticket twice, then one ticket three times, then all the way until ten times. Light bulbs started turning on in their brains and they realized that buying the 12 tickets for $5 was a better option than 10 tickets for $5 if bought one at a time. However the downside of this discussion was that it skewed their thinking process into only comparing similar rates for the rest of the period. Not a single student attempted a unit rate strategy. With more time or a second day, I would have guided them towards this strategy. However the period was almost over so we had a discussion about what we had found so far and I collected their Problem Solving Frameworks.
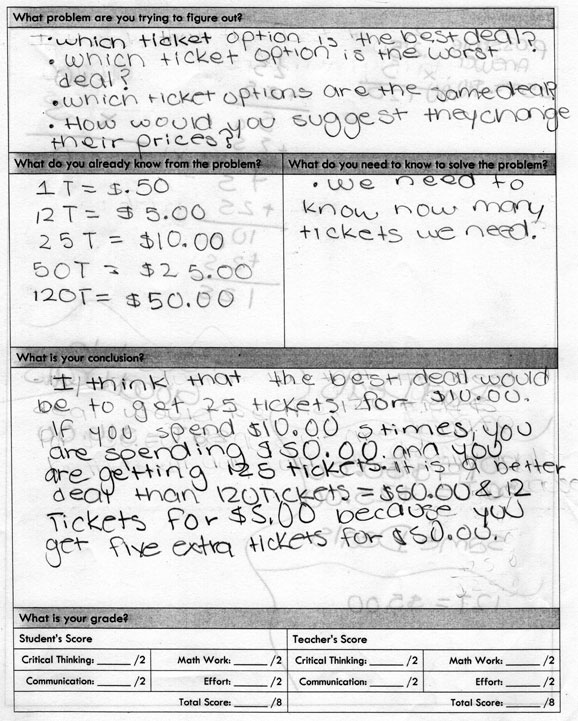
Virtually all students stated that the 25 tickets for $10 was the “best” deal. However in terms of providing “sufficient reasoning to support [their] conclusion” (which will be required by the CCSS assessments) there was a range of success. I have categorized students’ reasoning as demonstrated in the “What is your conclusion?” section as high, medium, and low. Clearly there is room for the highs to improve, but they do a much better job of articulating their mathematical understanding using precise language than the lows and mediums:
Low 1
Low 2
Medium 1
Medium 2
High 1
High 2
What are your thoughts? If you had a second day with these students, how would you guide them towards implementing a unit rate strategy? Do you disagree with any of my low, medium, high rankings?